
Au XVIIe siècle, le physicien néerlandais Isaac Beekman s’intéresse à la relation de causalité entre la Lune et les marées. Une observation rapportée près de Bordeaux va le conforter dans son hypothèse.
Mais d’abord qui est Isaac Beekman ? Isaac Beeckman (1588-1637) est un physicien, ingénieur et météorologue néerlandais peu connu. N’ayant pas publié de son vivant, son influence sur le développement de la science est méconnue. Elève de Simon Stevin, ami de René Descartes, qui a dédié sa première œuvre, le Compendium Musicae, à Beeckman, il est considéré comme l’un des scientifiques les plus éminents de son époque. En plus d’être médecin – il obtient sa thèse à l’université de Caen – il étudie les mathématiques et propose de donner à toute science et à toutes les connaissances une base solide, en prenant les mathématiques comme socle. Sa correspondance avec Marin Mersenne, Tycho Brahé, Johannes Kepler, Pierre Gassendi, Francis Bacon ou bien les docteurs William Gilbert et William Harvey montrent qu’Isaac Beekman était connu et reconnu par ses pairs.
Isaac Beekman a tenu un journal personnel de 1604 à 1635 où on découvre l’étendue de son champ de recherche et sa curiosité pour les phénomènes de la Nature. Il s’intéresse au vide où il s’oppose à la thèse aristotélicienne – la Nature a horreur du vide – et on trouve un petit article écrit entre les dates du 27 février et du 15 mars 1628 qui est assez croustillant sur l’influence de la Lune sur les marées.
Mais revenons aux thèses en vogue à l’époque sur l’explication des marées.
Que la lune soit à l’origine du mouvement de la mer est admis par tous les philosophes ; ils en donnent diverses explications.
Depuis longtemps, on attribuait la cause des marées aux rayons de la lumière lunaire. L’humidité était tenue pour l’effet propre de la Lune et plusieurs contemporains expliquaient le flux et reflux par une sympathie entre deux corps de même qualité. A côté de cette hypothèse on trouve aussi la théorie à base d’aimants des marées. L’idée de décomposer la marée totale en deux autres – l’une causée par le froid de la Lune, l’autre par la chaleur du Soleil – thèse qui fut surtout favorisée par les astrologues. Et laissons Beekman nous en parler à travers son Journal :
13 février 1625, la Lune émettrice d’humidité
Simon Stevin[1] pense qu’il existe des eaux très profondes là où la lune elle-même, ou son opposé, se trouve dans l’océan. Mais je n’en donnerai peut-être pas la raison physique de manière aussi complexe.
De même que le soleil est une source de chaleur, la lune l’est d’humidité ; le froid et la sécheresse ne sont que des privations pour elle. La lune émet donc perpétuellement de l’humidité : pourtant, elle n’est pas plus pauvre que le soleil en chaleur, et comme elle est proche de la Terre, il ne semble pas plus difficile pour elle de se nourrir d’humidité, c’est-à-dire d’eau, que le soleil, qui est beaucoup plus sublime, de feu, qui est beaucoup plus éloigné. La lune émet donc la plus grande quantité d’humidité dans l’air le plus proche d’elle, c’est-à-dire celui qui se trouve sur le même méridien ; puis elle en émet une quantité presque négligeable dans l’air opposé. Puisque l’humidité pénètre difficilement le feu, les rayons humides, effleurant à peine la surface de la Terre, sont réfléchis vers la surface de l’air. Comme cela se produit de toutes parts et que le rayon d’incidence est égal au rayon de réflexion, ils sont nécessairement déviés vers la partie de l’air directement opposée à la Lune, où convergent tous les rayons lunaires déviés par la Terre. En effet, tous ces rayons rendent la surface de l’air concave à des angles inférieurs à 90°.
Et si quelqu’un pense que l’air terrestre est si proche que les rayons réfléchis ne peuvent atteindre la face opposée de la Lune par une seule réflexion, il doit se rappeler que ces rayons, émis à une telle vitesse, une fois arrivés à destination, décrivent un cercle pendant un certain temps avant de s’y rencontrer et de remplir l’air. Mais les rayons qui pénètrent également le feu convergent plus haut et, de ce fait, sont déviés vers le bas d’un côté.
Nous avons déjà entendu dire que l’air mélangé à l’humidité devient plus raréfié et, par conséquent, a moins de poids pour comprimer l’eau. Mais l’air pur latéral, que seuls les rayons traversent, ne s’allège pas plus que ces rayons et conserve sa gravité, comprimant ainsi l’eau vers les endroits où, comme nous l’avons dit, l’air est devenu moins résistant. L’air, saturé d’humidité, se gonfle alors et ses parties supérieures descendent sur les côtés, d’où il comprime également l’eau avec l’aide de l’air entrant. Et même si cela ne se fait pas instantanément, cela se fait néanmoins progressivement et aisément. Car une fois l’air saturé d’humidité, l’endroit suivant se remplit successivement au gré du mouvement de la Lune. Ainsi, l’endroit se remplit facilement, car la matière est proche et le temps est suffisant pour favoriser ce changement d’emplacement.
Pour savoir si la Lune éjecte réellement de l’humidité, il serait peut-être possible de l’explorer à l’aide de miroirs ardents, après quoi tous les rayons seraient concentrés en un seul point. En effet, une grande quantité d’humidité apparaîtrait sur du papier sec, surtout si plusieurs miroirs de ce type sont dirigés vers le même point sur le papier. Mais si l’humidité de la Lune n’est pas suffisamment ténue pour traverser les pores du verre, il faut utiliser des miroirs catoptriques pour réfléchir les rayons vers le même point ; ou mieux encore, il faut fabriquer une pyramide de miroirs dont la surface intérieure est réfléchissante, mais la surface extérieure est recouverte ; et la partie la plus large, qui est son orifice, doit être opposée à la Lune, de sorte que les rayons de la Lune, collectés là avec l’humidité, puissent atteindre le cône intérieur et y humidifier une certaine particule du papier, si la Lune émet de l’humidité.
Si les explications de Beekman semblent obscures, avec une lune émettrice d’humidité via ses rayons, on remarque son effort de mathématisation du problème en invoquant les règles d’optique géométrique sur la réflexion et en proposant encore une fois une expérience pour valider son hypothèse sur la Lune émettrice d’humidité. Un peu plus tard, toujours dans son Journal, il poursuit avec une explication où de l’humidité est portée de la Terre vers la Lune grâce à l’action du Soleil, et comme la Lune est elle-même émettrice d’eau, les parties s’attirent ainsi.
4 mars 1627, les marées de pleine lune et de nouvelle lune
Puisque nous disons que l’humidité est drainée de la Lune par les rayons du Soleil, il est nécessaire d’expliquer également comment elle y est restituée.
Cela se produit particulièrement lors de la pleine lune et de la nouvelle lune. En effet, lors de la pleine lune, le Soleil, en érodant l’humidité de la Terre de part et d’autre, la transporte vers la Lune, c’est-à-dire sur ses côtés, au-dessus et en dessous. Mais quel que soit l’angle de vue de la Lune à ce moment-là, les rayons du Soleil, chargés de l’humidité terrestre, sont réfléchis par elle et transportent vers la Terre et les mers tout ce qu’ils peuvent par réflexion. À la nouvelle lune, l’humidité lunaire est alimentée par les rayons réfléchis du Soleil vers la Terre, lui apportant ainsi son humidité. Cependant, la Lune est constamment en contact avec des vapeurs humides dispersées dans son immense étendue, qui adhèrent à elle par congruence.
Il ne faut donc pas croire que, de ce fait, le mouvement perpétuel de la Lune, avec les vapeurs qui lui sont attachées, soit sensiblement ralenti. Car bien que ces humidités, au contact de la Lune, lorsqu’elles sont immobiles ou en mouvement contraire, semblent atténuer son mouvement, l’immense proportion entre la Lune et ces humidités réduit son mouvement sur des milliers d’années, le rendant imperceptible. Il ne serait peut-être pas absurde non plus d’attribuer à ce phénomène l’anomalie de mouvement du Soleil, de la Lune et des autres étoiles, cette anomalie, dis-je, que les astronomes ne peuvent expliquer par des règles et qui ne fut détectée que plusieurs siècles auparavant, telle que les modernes la découvrent et que les Anciens, même de manière obscure, l’observent.
De plus, non seulement la partie de la mer directement opposée à la Lune gonfle, mais aussi celle qui lui est opposée aux antipodes, selon l’opinion de Stevin. La raison en est que les rayons du Soleil, directs ou réfléchis, chargés d’humidité par la Lune et rasant les faces de la Terre, sont réfractés en sens inverse, transportant ainsi l’humidité soit vers les hautes couches de l’atmosphère, soit au-dessus ou au-dessous. Cette humidité est soit abandonnée là par le feu, c’est-à-dire par les rayons solaires, soit par le feu élémentaire ou d’autres rayons d’étoiles, etc., s’approchant de la Terre et étant emportés jusqu’à l’atteindre. Ainsi, la partie de la Terre sur laquelle reposent la Lune et son opposé se gorge d’humidité ; mais les côtés situés de part et d’autre non seulement ne reçoivent rien en raison de leur obliquité, mais aussi, au passage des rayons du Soleil, sont contraints de se délester de l’humidité qu’ils possèdent.
On voit que les lois de l’optique, qui occupent dans les mêmes années son compatriote Wilhelm Snell (il trouve la relation de la réfraction en 1621 sans la publier), mais aussi son ami René Descartes (il publiera ses lois en 1637 dans son traité La Dioptrique) sont au centre de son raisonnement mathématique.
Enfin, venons en à l’expérience décisive qui est rapportée à Isaac Beekman.
27 février – 15 mars 1628, la grotte cachée près de Bordeaux
J’ai entendu Gysbrecht[2] dire qu’à environ un demi-mille de Bordeaux, il avait vu une pierre surmontée d’un petit bassin, comme une coupelle. Ce bassin était toujours plein d’eau les jours de pleine lune, mais vide lorsque la Lune était au quartier.
Je pense que cela concorde en partie avec ce que j’ai écrit quelque part[3], à savoir que la lune elle-même apporte de l’humidité, tout comme le soleil apporte de la chaleur à son corps. Et de même que la chaleur du soleil, en pénétrant dans l’air, l’ouvre et l’élargit, de sorte qu’il occupe un plus grand volume, de même l’humidité de la lune, en pénétrant dans l’eau, la dilate et l’ouvre, et l’oblige également à occuper un plus grand volume.
Pour vérifier cette hypothèse, on prend un grand récipient rempli d’eau, fermé par un petit bassin ouvert placé au-dessus, et on le remplit d’eau jusqu’à mi-hauteur du bassin, qui n’a que la largeur de la pointe d’une aiguille. On observe alors si le niveau d’eau dans ce bassin est plus élevé à la pleine lune qu’aux quartiers ; il en va de même à la nouvelle lune, et même chaque jour, que la lune soit au sud ou au nord. Le récipient doit être énorme, car il doit exister une proportion similaire entre le volume du récipient et la largeur du bassin qu’entre l’Océan et la marée haute qui se forme dans l’Océan, dont on dit que le niveau d’eau y monte très peu, comme je l’ai écrit ailleurs[4].

Ainsi, aux abords de Bordeaux, on ne voyait que le récipient surmonté d’un pilier. Au fond du récipient, à travers le pilier et plus loin sous terre, se trouvait un orifice. À l’autre extrémité de cet orifice était placée une large corniche remplie d’eau. Lorsque la lune était pleine, l’eau s’écoulait par cet orifice dans le récipient.
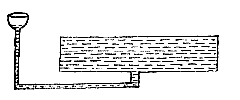
Cela concorde également avec ce que D. Colvius m’a dit, à savoir qu’à Venise, la distance est d’une trentaine de centimètres, ce qui, comme je l’ai expliqué précédemment, s’explique par le fait que toute la houle de la Méditerranée y est contenue et stagnante ; l’eau ne pouvant s’écouler, elle y reste, d’où la houle perçue.
Il est également possible qu’aux abords de Bordeaux se trouve une grande grotte souterraine remplie d’eau, qui ne peut s’échapper que par cet unique orifice. Si la lune dilate alors l’eau contenue dans ce trou, elle doit nécessairement s’écouler vers cette ouverture, où certains passionnés auraient pu installer un petit pont, surmonté d’un pilier et d’une petite soucoupe. Je crois avoir déjà écrit à ce sujet[5].
En 1628, Isaac Beekman utilise cette expérience pour valider une hypothèse qu’il a déjà faite sur la relation entre la Lune et les marées et l’attraction mutuelle entre l’eau et la Lune.
La grotte près de Bordeaux ?
Cependant, habitant la région bordelaise, je me demande de quelle grotte il s’agit. La seule grande grotte connue est à 25 km au nord de Bordeaux : la grotte de Pair-non-Pair de Prignac-et-Marcamps qui sera enregistrée dans un relevé cadastral en 1667, donc probablement déjà connue en 1628. Mais la configuration du système décrit par Beekman fait davantage penser à une grotte enclavée, de type nappe phréatique, or les nappes phréatiques sont des systèmes ouverts. La proximité avec la ville bordelaise (un demi-mille faisant environ 1km), peut nous emmener sur les coteaux de Lormont, Cenon ou Floirac qui sont faits de calcaire peu karstifiés datant du jurassique et fracturés, une configuration peu propice à la rétention de l’eau en formant de grands bassins. Les cavités répertoriées dans la région sont d’origine artificielle pour l’extraction industrielle du calcaire, ou des niches qui ont pu servir pour l’ermitage ou de refuges. Bref, le mystère de la localisation de cet endroit décrit par Beekman reste entier.
Bibliographie et webographie
Journal tenu par Isaac Beeckman,
Tome III, 27 février – 15 mars 1628, pp. 38-39
Tome II, 13 février 1625, pp. 317-318, 363-364, 387-388
https://www.dbnl.org/tekst/beec002jour03_01/beec002jour03_01_0003.php#p38
Site officiel de la grotte de Pair-non-Pair
https://www.pair-non-pair.fr/
Wikipedia, grotte de Pair-non-Pair
https://fr.wikipedia.org/wiki/Grotte_de_Pair-non-Pair
[1] Tomus primus Mathematicorum hypomnematum, Lugd. Bat., 1608, Secunda pars, pp. 175 sqq.
[2] Un ami dont nous savons peu de choses.
[3] Cf. t. II, pp. 317-318, 363-364, 383 et 387-388.
[4] Cf. t. II, pp. 229 et 363-364.
[5] Cf. t. I, p. 104.
L’image en avant a été générée avec l’I.A.

Laisser un commentaire