Petites histoires des sciences

Les premiers arpenteurs

Archytas de Tarente (428-347 av. J.-C.), dont Horace rend hommage comme « le mesureur de la terre, de la mer et des sables sans nombre », est parmi les premiers à proposer une méthode pour déterminer la taille de la Terre. On prend deux positions sur le même méridien et on observe quelles étoiles culminent au même moment au-dessus de ces positions. Si l’on mesure la différence angulaire entre deux étoiles comme une partie du méridien céleste et que l’on multiplie sa réciproque par la distance terrestre entre les positions, on obtient la circonférence de la Terre. Mais il ne semble pas avoir laissé de résultats.

Aristote (384-322 av. J.-C.), dans son traité Du Ciel, donne des arguments raisonnés en faveur de la forme sphérique de la Terre. Il mentionne les navires qui passent sous l’horizon ainsi que les étoiles qui sont plus ou moins hautes dans le Ciel lorsqu’on se déplace vers le Nord ou le Sud. Il rapporte même la première estimation de la circonférence de la Terre :

 « Et les mathématiciens qui ont essayé de mesurer les dimensions de la circonférence, la portent à quarante fois dix mille stades ».

Malheureusement, Aristote ne cite pas le nom de ces mathématiciens ni leurs méthodes. La longueur d’un stade a été sujette à de nombreuses recherches. On s’appuie sur l’article de Dutka pour les données tout au long de notre histoire et si on prend un stade pour 157,5 mètre, alors Aristote porte la circonférence de la Terre à 63 000 km, ce qui est au-delà de la circonférence retenue de nos jours pour une circonférence le long d’un méridien, qui est de 40 008 km.

Dans la seconde moitié du IVe siècle av. J.-C., le voyageur grec Pytheas de Massilia (Marseille) visite l’Espagne, la Bretagne, la Gaule et il note des données géographiques, astronomiques et autres concernant les lieux qu’il visite. Eratosthène de Cyrène (276 – 184 av. JC), directeur de la bibliothèque d’Alexandrie, étudie la description des voyages de Pytheas, et cela l’a peut-être influencé à utiliser une version améliorée du gnomon pour mesurer la taille de la Terre : le skaphe. Inventé par Aristarque de Samos, le fondateur d’un système mondial héliocentrique, Le skaphe est un bol hémisphérique avec une tige verticale centrée à sa base. La tige projette une ombre à l’intérieur du bol lorsqu’elle est éclairée par le Soleil. Ainsi, une mesure angulaire de l’ombre est obtenue au lieu d’une mesure de longueur avec le cadran solaire conventionnel.

La méthode d’Eratosthène

La méthode utilisée par Eratoshtène est décrite par Cléomède, astronome du I^e siècle av. J.-C., à la fin du premier livre de sa Théorie circulaire des corps céleste. Ce texte écrit en grec et traduit de nombreuses fois et je prends pour appui la version latine de Roberto Balforeo faite en 1605.

Traduction :

« Premièrement, il nous est admis que Syène et Alexandrie sont sous le même méridien, et que l’intervalle entre leurs villes est de cinq mille stades. Troisièmement, les rayons envoyés depuis différentes parties du soleil vers différentes parties de la terre sont parallèles car les géomètres considèrent qu’il en est ainsi. Quatrièmement, on suppose aussi, comme le démontre le géomètre, que les lignes droites incidentes sur des lignes parallèles font des angles alternés égaux les uns aux autres. »

Reprenons les hypothèses de travail sur lesquelles nous reviendrons plus tard :

1. Syène, aujourd’hui Assouan, et Alexandrie, villes situées en Egypte sont sur le même méridien.
2. Cléomède parle de 5000 stades, soit environ 787,5 km. 
3. Les rayons issus du soleil sont parallèles entre eux.
4. Une ligne droite sécante à deux lignes parallèles forme des angles alterne-internes.

Discutons rapidement de ces hypothèses.

1. Un petit œil sur Google Earth pour se rendre compte qu’Alexandrie et Syène ne sont pas exactement sur le même méridien.

2. Sur de très longues distances où les relevés n’existaient pas, le seul moyen possible d’obtenir des estimations de distance raisonnablement précises était le recours à des bématistes, des hommes entraînés à faire des pas réguliers lorsqu’ils marchaient d’un endroit à l’autre et à enregistrer leur nombre. Le mythe, selon lequel dans l’Égypte ancienne, la distance quotidienne parcourue par les caravanes de chameaux servait à estimer les longs voyages, n’est pas crédible. Les chameaux ont été introduits en Afrique du Nord à l’époque d’Alexandre, mais les caravanes de chameaux ne sont devenues courantes qu’à l’ère chrétienne.

Alors que vaut un stade ? Dans l’article de Dutka, on apprend qu’en 1975, Hultsch un philologue allemand, s’intéresse à la valeur d’un stade, qui variait d’une région à l’autre, parfois au sein d’un même pays. Il indique un passage de l’ouvrage de Pline qui assimile 40 stades à un schoenus dans l’ouvrage d’Eratosthène La mesure de la terre (In libri dimensionum). En prenant un schoenus comme étant égal à 12 000 coudées et une coudée comme étant égale à 0,525 m, Hultsch estime, à partir de preuves archéologiques, le stade d’Eratosthène à 157,5 m. Sa valeur, confirmant les estimations antérieures d’autres personnes, a été acceptée par la plupart des éminents érudits du début du XXe siècle, bien qu’elle ne soit basée que sur une seule référence dans la littérature antique. Plus loin, Pline tente de convertir le stade d’Eratosthène en mesure romaine et utilise l’équivalent de 185,6 m pour un stade. Mais cette dernière valeur n’est devenue largement utilisée qu’à l’époque impériale romaine, plusieurs siècles après Eratosthène. En 1982 et 1987, deux articles de Rawlins et Gulbekian traitent de la valeur du stade, et ils donnent des valeurs mutuellement contradictoires : Rawlins donne 185 m, le stade olympique, tandis que Gulbekian en déduit 166,7 m. On prend la mesure de Hultsch pour la suite.

3. Le Soleil émet des rayons dans toutes les directions. Pour qu’ils puissent être considérés comme parallèles, il faut supposer que la distance entre le Soleil est très grande. Eratosthène est contemporain d’Aristarque de Samos, dont il connaissait les travaux. Aristarque avait démontré que le Soleil était très éloigné de la Terre.

4. Ce n’est pas ici une hypothèse mais un petit théorème mathématique de niveau collège.

Poursuivons le texte :

« Il dit donc, et c’est vrai, que Syène est sous le tropique d’été. Lorsque le soleil se couche en Cancer, faisant ses inversions estivales, il atteint le milieu du ciel, l’ombre des gnomons des horloges est nulle, le soleil étant placé au-dessus du corps. Mais à Alexandrie, à cette même heure, les gnomons des horloges projettent leur ombre. »

Rappelons ce qu’est un tropique : c’est un cercle imaginaire parallèle à l’équateur et situé à environ 23,5° de latitude. Les inversions estivales dont parle Cléomède sont les solstices. Et en été, ce jour là, autour du 21 juin, le Soleil est au plus haut dans le ciel, soit au zénith. Aux tropiques, un gnomon, tige tenue verticalement et qui sert à donner l’heure, ne projette alors aucune ombre. Pour toute ville située plus au Nord, une ombre existe. Au passage, dans l’hémisphère Nord on parle de Tropique du Cancer car le Soleil couchait dans la constellation du Cancer au solstice d’été dans l’Antiquité. Pour l’hémisphère Sud, vous l’aurez compris, le Soleil se couche dans la constellation du Capricorne pour leur solstice, soit autour du 20 décembre.

Poursuivons :

« Si nous réfléchissons plus loin, des lignes droites traversent la terre des deux côtés ; rejetée par le gnomon, elle converge vers le centre de la terre. Donc, puisque l’horloge, qui se trouve dans la ville de Syène, est sous la perpendiculaire du soleil, si l’on entend la droite partant du soleil, venant au sommet du gnomon de l’horloge, la droite allant du soleil à les autres terres ne feront plus qu’un point. »

Roberto Balforeo commente l’œuvre de Cléomède et le procédé de mesure d’Eratosthène. Il propose, page 220, le schéma suivant :

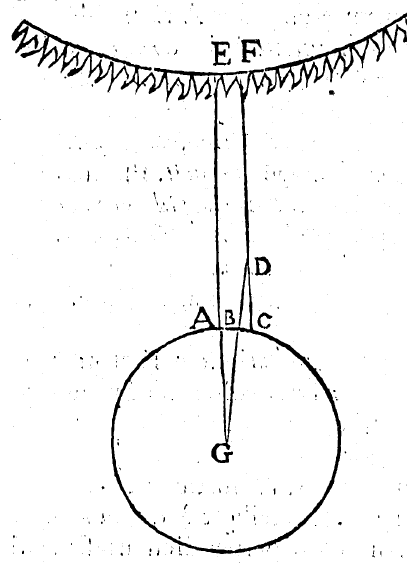
Syène est donc la lettre A et Alexandrie la lettre B. Le segment BD représente un gnomon dont l’ombre projetée sur le sol est le segment BC. Le gnomon est vertical, or une ligne verticale passe forcément par le centre de la Terre, ici en G. Cet angle est celui mesuré au sommet D du triangle BDC. Par la propriété des angles alterne-internes, c’est également l’angle au sommet G du triangle AGB.

Eratosthène observe son scaphe à Alexandrie :

« Or, ce qui se trouve au bord du Scaphe donne la cinquantième partie du cercle. »

Rappelons qu’un scaphe permet d’obtenir une mesure angulaire : La tige projette une ombre à l’intérieur du bol lorsqu’elle est éclairée par le Soleil. Ainsi, une mesure angulaire de l’ombre est obtenue. Ici, on obtient la cinquantième partie d’un cercle soit 360 / 50 = 7,2°

La distance Alexandrie-Syène étant connue, 787,5 km, elle correspond donc à un angle de 7,2°. Par proportionnalité, on peut calculer la circonférence, soit : 39 375 km. Ce qui est remarquablement proche de la valeur admise actuellement, environ 40 000 km.

La méthode d’Eratosthène est entachée de nombreuses incertitudes de mesures, comme la mesure de la distance entre les villes par les bématistes et le fait que les villes ne sont pas sur le même méridien. Cependant, ces erreurs se sont compensées pour offrir un résultat cohérent.

La démarche présentée ici est au programme des classes de 1ère dans l’enseignement scientifique. D’autres histoires avec leurs calculs sont présentés dans mon livre disponible aux éditions Ellipses 🙂

---

Références bibliographiques et webographiques

Aristote, Du Ciel, livre II, Chapitre 14, proposition 16.
https://fr.wikisource.org/wiki/Trait%C3%A9_du_Ciel/Livre_II

Cleomède, Cleomedis Meteora, graece et latine, traduite par Roberto Balforeo, 1605.
https://gallica.bnf.fr/ark:/12148/bpt6k94860v

Cléomède, Théorie élémentaire (De motu circulari corporum caelestium), éd. Richard Goulet. In: Revue d’histoire des sciences, tome 35, n°2, 1982. pp. 165-167
https://www.persee.fr/doc/rhs_0151-4105_1982_num_35_2_1825

Dutka, J. (1993). Eratosthenes’ measurement of the earth reconsidered, Archive for History of Exact Sciences, 46(1), 55–66.
https://doi.org/10.1007/BF00387726 

Horace, Odes, Livre I, poème 28
https://www.stilus.nl/horatius/HorCarI-28TeMarisEtTerrae.htm

L’image en-avant a été générée par IA.